open pose

paper
code

一般多人姿态估计都是使用人体检测器，然后再进行姿态估计的方法，这种方法不可靠，同时，人越多，计算量越大。相比较，自下而上的方法就很鲁棒。但是自下而上的方法并没有直接使用全局上下文线索。比如，deepcut这个方法提出了联合地标记身体部件和将身体部件联系成一个人上。但是解全连接图上的整数线性规划问题是一个NP难的问题并且处理时间非常久。后来的deepercut虽然使用了ResNet和依赖图像的pairwise scores并且极大的提高了速度，但是还是很慢，并且proposals的数目有限制。

本文提出了一种有效的多人姿态估计的方法，融合了检测部件位置和身体部件之间的联系的处理框架。自底向上推理，逐像素分析。

系统以w*h的图片作为输入，最后输出的是图片中每个人的关键点的2D位置。如图所示，一个前馈网络同时预测身体部位位置产生一组2D置信图(confidence maps)S,和一组身体部位关系的2D矢量L，它同时融入了身体部位联系的程度。
其中$\textbf{S}=(\textbf{S}_1,\textbf{S}_2,…,\textbf{S}_J)$一共有J个置信图，每个身体部位一个，且$\textbf{S}_j\in R^{w*h},j\in {1…J}$这里表示的是对图片的每个像素有一个概率，表示它是不是属于身体部位的一部分，也就是每个身体部位都单独生成了一个置信图
而$\textbf{L}=(\textbf{L}_1,\textbf{L}_2,…,\textbf{L}_C)$一共有C个矢量，同样是每个身体枝干一个，而$\textbf{L}_c\in R^{w*h*2},c\in {1…C}$。枝干的关系自然是必须包含两个身体部位之间的关系，所以需要的是w*h*2。文章说每个图片的位置在$L_c$中都编成2D矢量，2D矢量是指PAFs包含了位置和方向双重信息，所以需要二维矢量。最后就是分析置信图和身体部位联系场来最终给出图片中所有人的关键点的位置。

论文框架

如上图所示，图片首先由一个传统的网络分析处理生成一组feature maps F作为第一阶段的输入。网络的每个阶段都被分成两个分支，上面一个检测身体部位置信图，下面一个预测部位与部位之间关系的联系场，
每一个分支都是一个迭代预测过程。在第一阶段，网络产生一组检测的置信图$\textbf{S}^1=\rho^1(\textbf{F})$和一组联系场$\textbf{L}^t=\phi^1(\textbf{F})$。$\rho^1$和$\phi^1$都是表示经过CNN的处理。
而在之后的阶段都会将前一阶段的置信图和联系场加上原始的VGG-19产生的feature maps一起来微调预测结果使其更精确，其公式如下：

$$\textbf{S}^t=\rho^t(\textbf{F},\textbf{S}^{t-1},\textbf{L}^{t-1}),\quad \forall t\geq 2,\qquad (1)$$ $$\textbf{L}^t=\phi^t(\textbf{F},\textbf{S}^{t-1},\textbf{L}^{t-1}),\quad \forall t\geq 2,\qquad (2)$$

按照文章所说，每个阶段都有一个监督，说的应该是每次损失函数将其与基准的位置进行比较吧。
也就是按照下图所示：

虽然开始可能存在错误，但经过多次的微调，上图第一行的右手手腕检测越来越正确，而左手的手腕显示的效果在削弱。第二列显示的是右前臂的检测效果，感觉看的不是很明显。
文章也就是对每个分支在其结尾处应用两个损失函数$L_2$来评估预测的位置以及关系与基准的差别。其评估公式如下：

$$f_S^t=\sum_{j=1}^J\sum_p\textbf{W}(\textbf{p})*||\textbf{S}_j^t(\textbf{p})-\textbf{S}_j^*(\textbf{p})||_2^2,\qquad (3)$$ $$f_L^t=\sum_{c=1}^C\sum_p\textbf{W}(\textbf{p})*||\textbf{L}_c^t(\textbf{p})-\textbf{L}_c^*(\textbf{p})||_2^2,\qquad (4)$$

其中，$\textbf{S}_j^*$和$\textbf{L}_c^*$分别表示基准的部位置信图和基准的部位联系矢量场。而$\textbf{W}$是一个二元掩膜，简单来说如果该位置被标记，
则$\textbf{w}(p)=1$否则$\textbf{w}(p)=0$。mask的目的是避免惩罚在训练过程中的正确的预测因为在实际的数据集中并没有标记人的全部信息。最终的目标函数：

$$f=\sum_{t=1}^T(f_S^t+f_L^t)\qquad (5)$$

Confidence Maps for Part Detection

从(5)中可以看到，训练过程中的基准$\textbf{S}^*$和$\textbf{L}^*$也是通过一定规则计算的。置信图$\textbf{S}^*$就是通过标记的2D关键点获得。每个置信图就是一个2D的置信度表示关于身体的某一特殊部位是否出现在每个像素的位置。对于每个2D表示的置信度，每个人的每个可见的身体部位都应该有一个峰值。
让$x_{j,k}\in R^2$表示图片中第k个人第j个身体部位的基准位置，在$\textbf{p}\in R^2$位置的基准值可通过下式获取：

$$\textbf{S}_{j,k}^*(\textbf{p})=exp(-\dfrac{||\textbf{p}-\textbf{x}_{j,k}||_2^2}{\sigma^2})\qquad (6)$$

用高斯函数产生的ground truth热图。
也就是将高斯函数的峰值放在被标记的关节点的位置获取。而最终的基准置信图是通过每个人的置信度的最大化操作获取：

$$\textbf{S}_{j}^*(\textbf{p})=\max_k\textbf{S}_{j,k}^*(\textbf{p})\qquad(7)$$

该公式的含义是如果图片中有多个人在p位置处重合的话，取其中的最大值。同时检测身体部位候选时采用了非最大值抑制。这样操作的结果就是当有多个人的部位重合的时候，只能检测出得分最高的那个人。

Part Affinity Fields for Part Association

知道了身体部位的位置，下一步自然是如何将这些部位连接起来，特别是当一幅图像中存在多个人的情况下如何判断哪些部位是属于同一个人的。一个可能想到的方法是检测每对部位的中间点是不是也在枝干上，并检测它在候选的部位上的发生率。然而当很多人拥挤在一起的时候，常常会导致错误的连接，如下图中的(b)。

可以看出仅知道部位的位置是不够的，同时如果仅仅是单个位置点的话也无法预判属于哪个枝干后面这个问题说的应该是对于单个检测部位的归属问题。
为了解决上述问题因此引入了一种新的特征表示方法也就是PAFs(part affinity fields)，它同时保存了支持枝干的位置和方向信息，如上图(c)所示。应该是每个枝干对应着一个2D的向量场，2D向量将枝干的一端到另一端的方向融入，因此每个类型的枝干都有一个对应的联系场连接着身体的两个部位。
考虑如下的单个枝干，$x_{j_1,k}$和$x_{j_2,k}$分别表示图片中第k个人的第c个枝干部位$j_1$和$j_2$的基准位置。如果一点$\textbf{b}$在这个枝干上的话，$\textbf{L}_{c,k}^*(\textbf{p})$表示一个从$j_1$指向$j_2$的单位向量。而对所有其他的点，则都为0.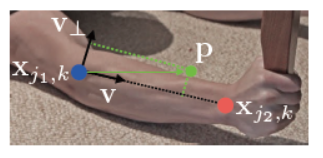

根据下式定义基准的部位联系向量场，则图片上一点$\textbf{p}$的值为：

$$\textbf{L}_{c,k}^*(\textbf{p})=\begin{cases} \textbf{v}\quad if\ \textbf{p}\ on\ limb\ c,k\\\textbf{0}\quad otherwise.\end{cases}\qquad (8)$$

其中，$\textbf{v}=(x_{j_2,k}-x_{j_1,k})/||x_{j_2,k}-x_{j_1,k}||_2$是沿着枝干方向上的单位向量。在该枝干上点都被定义为满足$\textbf{v}=(\textbf{p}-x_{j_1,k})\leq l_{c,k}\ and\ |\textbf{v}_\bot *(\textbf{p}-x_{j_1,k})|\leq \sigma_l,$的线段。
而基准部位联系场采用平均图片中所有人的联系场，如下式：

$$\textbf{L}_{c}^*(\textbf{p})=\dfrac{1}{n_c(\textbf{p})}\sum_k\textbf{L}_{c,k}^*(\textbf{p})\qquad (9)$$

其中$n_c(\textbf{p})$表示在$\textbf{p}$处所有非0的数量。
在测试阶段，我们测量候选部位的联系通过计算与他们相关PAF的线积分，其是通过线段连接的候选部位的位置。换句话说，我们测量预测的PAF和候选枝干的匹配，而候选的枝干就是通过连接身体部位而组成的。明确来说，
对于两个候选部位$\textbf{d}_{j_1}$和$\textbf{d}_{j_2}$，我们采样已经预测的部位联系场，沿着线段方向$L_c$的来计算他们关系的置信度：

$$E=\int _{u=0}^{u=1}\textbf{L}_{c}(\textbf{p}(u))\cdot \dfrac{\textbf{d}_{j_2}-\textbf{d}_{j_1}}{||\textbf{d}_{j_2}-\textbf{d}_{j_1}||_2}du,\qquad (10)$$

而$\textbf{p}(u)$通过下式得到：

$$\textbf{p}(u)=(1-u)\textbf{d}_{j_1}+u\textbf{d}_{j_2}\qquad (11)$$

在实际中，近似求解积分通过采样求和等距的u.

Multi-Person Parsing using PAFs

当图片存在很多人的时候，对所有的关键点如果都要利用式(10)计算枝干的话将是非常耗时的。定义$z_{j_1,j_2}^{mn}\in {0,1}$
来预测两个候选检测部位$\textbf{d}_{j_1}^m$和$\textbf{d}_{j_2}^n$是不是连接的，其中表示第j个身体部位的第m个候选检测的位置。
最终的目的就是在所有的可能的连接中找到最优的匹配，

$$Z=\{z_{j_1,j_2}^{mn}:for\ j_1,j_2\in \{1...J\},m\in \{1...N_{j_1}\},n\in \{1...N_{j_2}\}\}$$

其中$N_j$表示第j个部位的候选个数。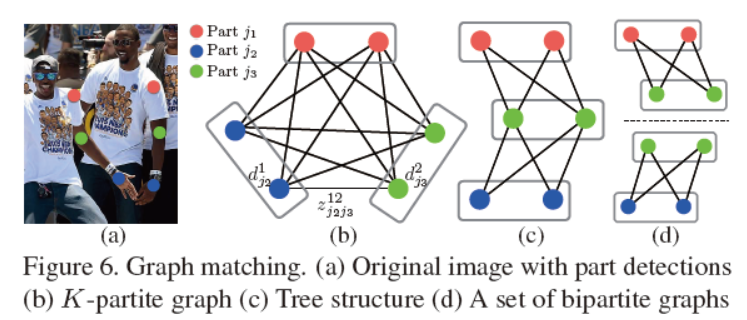

如图(b)所示，如果按照图的匹配方法，需要计算的量很大，图中每条边的值通过(10)计算。
在二分图中的匹配是遵循没有两个边共享同一个节点的原则选取的，
所谓的二分图说的是对检测某一个枝干而言，因为有多个人，所以比如左手臂自然会有多个需要检测，所以任何两个枝干是不可能有重合的最终的目的就是对于选取的边根据最大权重找到相应的匹配：

$$\max_{Z_c} E_c = \max_{Z_c} \sum_{m \in D_{j_1}} \sum_{n\in D_{j_2}} E_{mn} \cdot z_{j_1,j_2}^{mn} \qquad(12)$$ $$s.t.\qquad \forall m\in D_{j_1},\ \sum_{n\in D_{j_2}}z_{j_1,j_2}^{mn}\leq 1,\qquad (13)$$ $$\qquad \quad \ \ \ \forall n\in D_{j2},\ \sum_{m\in D_{j1}}z_{j_1,j_2}^{mn}\leq 1,\qquad (14)$$

其中, $E_c$ 是枝干c的匹配的整个权重, $Z_c$ 是整个Z中关于枝干c的子集，而$E_{mn}$是由(10)计算两个部位$d_{j_1}^m$和$d_{j_2}^n$的联系，公式(13)和(14)确保没有两个边共享一个节点，按照文章中说的是，同种类型的两个枝干不会共享同一个节点。
由上图(b)可以看到，如果看成b维的匹配问题的话将会是一个NP难的问题，同时有很多松弛存在。这里论文做了两个进一步的处理，选择最小数量的边使其能够表示
整个人的姿态的框架，如图(c)所示。二是进一步将问题分解为一组双边匹配的子问题，分别在检测连接树节点的匹配问题，如图(d)所示。
通过上述的两个松弛，优化问题最终被分解为:

$$\max_Z E=\sum_{c=1}^C\max_{Z_c}E_c,\qquad (15)$$

首先通过式(12)(13)(14)来计算各个枝干连接的候选，通过计算出来的所有的枝干候选，通过(15)我们可以整合所有的分享同一个部位的枝干从而获取多个人的整个身体的姿态。

the state of the art