论文:
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
Batch Renormalization: Towards Reducing Minibatch Dependence in Batch-Normalized Models
一、batchnormalization简介
1.源起
Internal Covariate Shift

简而言之就是:在网络训练过程中,随着网络层数加深,网络的输入会很大,跑到激活函数的饱和区,使得梯度消失。我们定义:在训练时因为网络参数的改变而导致的网络激活的输出的分布的改变,成为内部协变量漂移。
问题
- 学习率要很小
- 初始化要谨慎
- 容易非线性饱和
2.bn做法
normal operation

For instance, normalizing the inputs of a sigmoid would constrain them to the linear regime of the nonlinearity. To address this, we make sure that the transformation inserted in the network can represent the identity transform. To accomplish this, we introduce, for each activation x(k), a pair of parameters
γ(k), β(k), which scale and shift the normalized value.
相对于普通标准化,这里引入两个变量:$\gamma,\beta$,为了让输出不仅仅是在非线性激活的过原点附近的线性区(以sigmod激活为例).为了适当保留其非线性,使用这两个参数进行分布的调整,至于调整多少,由训练决定。
bn in cnn

cnn层的输出是4维tensor, [B, H, W, C], B 是batch size, (H, W) 是 feature map大小, C 通道数. 其中索引 (x, y) , 0 <= x < H 和 0 <= y < W 是空间位置spatial location.
usual bn
是使用B元素计算出H*W*C 个均值和 H*W*C标准差 .即不同层的不同位置的元素有自己的均值和标准差(B个元素计算出的).
cnn bn
cnn的参数对于整张input图像共享。所以我们将每张特征图看作是一个激活,也就是使用B*H*W个元素计算C个均值和方差。
3.bn反传
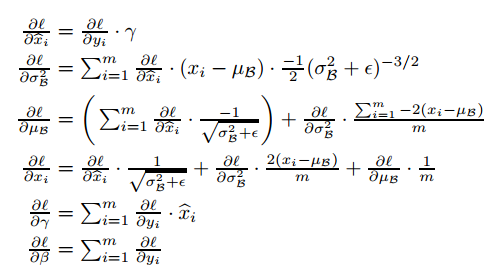
4.bn训练和推断过程

二、some questions
1.Training vs Testing
- 训练过程中,需要计算出mini-batch的均值和标准差来规范化该batch,同时使用moving average的方式计算population mean和variance,以供测试时使用。
- 在inference时,使用预先计算出来的参数进行mini-batch的统计。
moving average的计算入下:
1 | running_mean = momentum*running_mean+(1-momentum)*sample_mean |
2.关于偏置
使用batch-normalization之后,不需要偏置b,因为任何偏置最后都会因为正规化输出而被被cancel掉,也就是偏置是无法学习的。
3.Batch Normalization as Regularization
dropout是网络训练正则化的一项重要手段:
- 它引入了噪声,因此使得网络在训练过程中能够学习处理这些噪声,因而能够泛化的更强。
- 另一个角度是:类似于bagging的思想,每次随机取0.5的数据,且数据不尽相同,可以大大提高模型的泛化能力。
batch-norm恰巧在训练时候也有引入噪声的功效:

解释是:
将dropout看成加入了一个噪声向量[0,0,0,1,1,……0],早就有论文论证过在梯度中加入噪声可以提高模型的accuracy。Adding Gradient Noise Improves Learning for Very Deep Networks
batch-norm和dropout类似,他在训练过程中给每个隐层单元乘上随机值。这个随机值便是mini-batch中的标准差,因为每个minibatch的数据都是随机挑选的,因此标准差也随机波动。同时也会减去一个随机的均值。
deep-understanding-of-batchnorm
4.Benefits
- 网络训练的更快:虽然训练过程中,额外的正则化参数和超参数(rescale,recenter)计算,但是网络收敛的更快。所以网络能够训练的更快。
- 可以使用更大的学习率:梯度下降需要学习率很小保证网络能够收敛。当网络变得更深的时候,梯度在后向传播的时候就会变得很小,需要迭代次数也更多。使用bn之后,可以提高学习率,加快训练。
- 权重初始化更简单:bn能够减少初始权重的敏感度。
- 可以使用更多的激活。
- 创建深层网络的方式更加简单。
- 一定程度正则化。
5.why use mini-average rather than moving average in training
It is natural to ask whether we could simply use the moving averages µ, σ to perform the normalization during training, since this would remove the dependence of the normalized activations on the other example in the minibatch. This, however, has been observed to lead to the model blowing up. As argued in [6], such use of moving averages would cause the gradient optimization and the normalization to counteract each other. For example, the gradient step may increase a bias or scale the convolutional weights, in spite of the fact that the normalization would cancel the effect of these changes on the loss. This would result in unbounded growth of model parameters without actually improving the loss. It is thus crucial to use the minibatch moments, and to backpropagate through them.
出自:Batch Renormalization: Towards Reducing Minibatch Dependence in Batch-Normalized Models
解释一下:在原论文中有一段话,说了如果激活函数的bn的计算不依赖于minibatch中的其他元素,那么会导致模型爆炸。
However, if these modifications are interspersed with the optimization steps, then the gradient descent step may attempt to update the parameters in a way that requires the normalization to be updated, which reduces the effect of the gradient step. For example, consider a layer with the input u that adds the learned bias b, and normalizes the result by subtracting the mean of the activation computed over the training data: xb = x - E[x] where x = u + b, X = {x1…N } is the set of values of x over the training set, and E[x] = N1 PN i=1 xi. If a gradient descent step ignores the dependence of E[x] on b, then it will update b ← b + ∆b, where ∆b ∝ -∂ℓ/∂xb. Then u + (b + ∆b) - E[u + (b + ∆b)] = u + b - E[u + b].
Thus, the combination of the update to b and subsequent change in normalization led to no change in the output of the layer nor, consequently, the loss. As the training continues, b will grow indefinitely while the loss remains fixed. This problem can get worse if the normalization not only centers but also scales the activations. We have observed this empirically in initial experiments, where the model blows up when the normalization parameters are computed outside the gradient descent step.
原本第m个mini-batch的均值计算如下:
比如说,我们更新了一个参数
而采用普通的moving average(非batch renormalization中的moving average计算方式)之后的bn之后的:
其中$\mu_m$是前面所以mini-batch的平均值,和本次$x$的更新无关。
所以
emmmmmmmm,推不下去了,反正意思就是说,使用滑动平均的话,其均值就会不依赖于本次mini-batch中的其他数据(我觉得意思就是,这个均值相当于是个定值???)。但是!这会使得normalization和SGD的过程混杂在一起,抵消了SGD的梯度更新的作用!比如,上面引用中说的,梯度更新使得某个参数:比如偏置更新了,或者缩放了权重,但是normalization之后其输出根本没变化,即更新参数之后对激活的输出没有影响,也即loss不会改变。最后模型参数就会无限增长,导致模型爆炸。